Review
Areti Angeliki Veroniki1,2,3, Sofia Tsokani1, Evangelos Paraskevaidis4, Dimitris Mavridis1,5
1Department of Primary Education, School of Education, University of Ioannina, Ioannina, Greece
2Knowledge Translation Program, Li Ka Shing Knowledge Institute, St. Michael’s Hospital, Toronto, Ontario, Canada
3Institute of Reproductive and Developmental Biology, Department of Surgery & Cancer, Faculty of Medicine, Imperial College, London, United Kingdom
4Department of Obstetrics and Gynaecology, Ioannina University Hospital, Ioannina, Greece
5Paris Descartes Université, Sorbonne Paris Cité, Faculté de Médecine, Paris, France
Correspondence: Areti Angeliki Veroniki, MSc, PhD, Research Fellow at the Department of Primary Education, School of Education, University of Ioannina, Ioannina, Greece. Tel.: +30 26510 05694, Fax: +30 26510 05854, e-mail: averoniki@uoi.gr
Abstract
Systematic Reviews of diagnostic test accuracy (DTA) studies are increasingly comparing the accuracy of multiple tests to facilitate selection of the best performing test(s). Common approaches to compare multiple tests include multiple meta-analyses or meta-regression with the test type as a covariate. Within-study correlation between tests are typically not considered in these approaches. Several DTA network meta-analysis (DTA-NMA) models have been suggested to compare the accuracy of multiple index tests in a single model. Our aim was to identify all DTA-NMA methods for comparing the accuracy of multiple diagnostic tests.
We conducted a methodological review of the DTA-NMA models. We searched PubMed, Web of Science, and Scopus from inception until the end of July 2019. Studies of any design published in English were eligible for inclusion. We also reviewed relevant unpublished material. The methods were applied in a network of 37 studies comparing human papillomavirus (HPV) DNA, mRNA, and cytology (ASCUS+/ LSIL+ threshold) for the diagnosis of invasive cervical cancer (CIN2+).
We included 10 relevant studies, and identified four Bayesian hierarchical DTA-NMA methods including the 2×2 data table for each index test. Using CIN2+ as a case study, we applied the DTA-NMA methods to determine the most promising test, in terms of sensitivity and specificity. All models showed the mRNA test as the most accurate test followed by HPV DNA: relative sensitivity compared to the cytology test 1.36-1.39 and 1.33-1.35, respectively. However, both tests had similar or worse specificity than cytology (relative specificity range in mRNA 0.96-0.98 and in HPV-DNA 0.94-0.95). Both sensitivity and specificity of mRNA were associated with the highest uncertainty across all models (widest 95% credible intervals 0.68-0.97 and 0.74-0.94, respectively). Precision and estimation of between-study and within-study variability vary across models, which might be due to the differences in the key properties of the models.
Different DTA-NMA methods may lead to different results. The choice of a DTA-NMA method for the comparison of multiple diagnostic tests may depend on the available data, e.g., threshold data, as well as on clinically-related factors.
Keywords: Network meta-analysis, diagnostic test, accuracy, indirect comparison, colposcopy
Introduction
Clinicians and healthcare professionals often consult diagnostic test accuracy (DTA) meta-analyses to make informed decisions regarding the optimum test to choose and use for a given setting1-3. Most DTA meta-analyses focus on the accuracy of a single test (i.e., an index test vs. the reference standard). Although direct test comparisons (head-to-head DTA comparisons) have the most valid design, they are not always available. The accuracy of different tests can be compared indirectly through a common comparator test.
When multiple tests exist for a given condition, selection of the best performing test is usually achieved by doing multiple meta-analyses and then comparing the results (i.e., pooled estimates and confidence intervals [CIs]). However, the tests in this approach are compared between different meta-analyses rather than within a single model, and there is no ‘borrowing strength’ across studies, especially when comparative studies of the underlying tests exist. Another popular approach is the meta-regression with the test type used as a covariate. This model statistically compares the accuracy of two or more index tests within a single meta-analysis, but it does not account for the within-study correlation between tests (i.e., due to the inclusion of the same individuals across tests) and the variance-covariance matrix is structured assuming independence between tests.
Network meta-analysis (NMA) of interventions combining both direct and indirect evidence within a single model is often used to inform clinical practice4-6. However, methods for conducting NMA of interventions cannot be applied directly for the comparison of multiple tests. This is mainly due to the design differences between studies comparing index tests and studies comparing interventions. Two key differences are that DTA-NMA focuses on two quantities, sensitivity and specificity, whereas NMA of interventions models a single effect size (e.g., odds ratio) and that intervention studies compare independent groups of patients, whereas DTA evaluate the same individuals across tests.
Several meta-analytical models were introduced for the comparison of the accuracy of at least two index tests against a reference standard in recent years7-17. NMA compares the accuracy of at least three index tests in a single model. DTA-NMA allows for obtaining more precise estimates, drawing inference on the accuracy of tests that have not been compared to each other before, and ranking tests according to their diagnostic accuracy (e.g. sensitivity [the probability of a test being positive when someone has the disease], specificity [the probability of a test being negative when someone does not have the disease])18.
Cervical cancer is the 4th most frequent cancer in women worldwide, including Greece, and can impact a woman’s reproductive years19. In 2018, approximately 311,000 women died from cervical cancer19. Since the development of the Papanicolaou test, screening has been used to diagnose cervical cancer at a stage that can be treated. In most cases, human papillomavirus (HPV) infection will be eliminated by the immune system. However, when the immune system does not clear the virus, HPV infection may develop abnormal cervical cells, known as cervical ‘precancer’20. These lessions can progress to cervical cancer if left untreated21. To this end, several studies were conducted to identify the best screening strategy for cervical cancer, including tests of cytology, HPV-DNA, mRNA, and co-testing (Pap test + HPV DNA or mRNA test)21,22.
To date, no studies have evaluated the accuracy of multiple tests for the diagnosis of cervical cancer in a single model to indicate the best diagnostic strategy. A hierarchy according to the test accuracy would help avoid unnecessary screening, colposcopy, and treatment (e.g., surgery) associated with undesirable effects, such as preterm births and miscarriages at 2nd trimester22.
In this study we aim to summarize the DTA-NMA methods for at least three index tests presented in the methodological literature17. We illustrate the application of the methods using a real data set for the comparative accuracy of HPV DNA, HPV mRNA, and cytology tests for cervical cancer.
Methods
Review methods
We searched PubMed, Web of Science, and Scopus from inception until the end of July 2019 to identify full text research articles that describe a DTA-NMA method for three or more index tests. Since joint classification of the results from one index against the results of another index test amongst those with the target condition and amongst those without the target condition are rarely reported in DTA studies, we included only methods requiring the 2×2 tables of the results of each index test against the reference standard (i.e., number of true positives, true negatives, false positives, and false negatives). Hence, we excluded DTA-NMA methods requiring the complete cross-tables (i.e., 2×4 joint classification tables). We scanned reference lists of the included studies for potentially relevant articles and conference abstracts, as well as searched on the web search engine Google. We used our networks of professional collaborations for additional studies, dissertations and ongoing research. Eligible studies were published and unpublished studies written in English that reported the development of a DTA-NMA method. The PubMed search strategy is included in Appendix 1.
Following a calibration exercise, pairs of reviewers (ST, SZ, IP, AAV) independently screened each title and abstract of the literature search results (level 1) and the full-text of potentially relevant articles (level 2) using the abstrackr tool (http://abstrackr.cebm.brown.edu/account/login). Conflicts were resolved by discussion. Once the screening process was completed, we recorded and discussed any conclusions or judgements on the performance of the methods as described by the authors.
The dataset
We illustrate the identified DTA-NMA methods using data from a recent Cochrane review by Koliopoulos et al23. This systematic review originally included 37 studies comparing 15 different tests for the diagnosis of invasive cervical cancer (CIN2+). These tests were recoded into three broader index tests (183,561 participants): human papillomavirus (HPV) DNA, mRNA, and cytology (ASCUS+/ LSIL+ threshold) (Appendix 2). Since not all of the included models evaluate different test thresholds, for studies reporting results on cytology at both LSIL+ and ASCUS+ thresholds we selected the latter. Colposcopy and/or histology was the reference standard. The full data set is provided in Appendix 2. The grey highlighted studies in Appendix 2 show the additional threshold data that could be included in the variance component model, compared to the remaining models. As commonly encountered in DTA studies, the full cross-tabulation data (i.e., 2×4 joint classification tables by pair of index tests in the diseased and non-diseased groups) were not available and used the available 2×2 table for each index test.
Figure 1 depicts the network plot of the three index tests, and shows that one study assessed cytology, 32 studies compared the HPV DNA test against cytology, and four studies compared HPV DNA versus cytology versus mRNA.

Figure 1. Network plot of cytology, HPV DNA, and mRNA tests for CIN2+. Circles correspond to the different tests, and edges represent studies comparing the connected tests. Solid edges correspond to triple-test studies, whereas the dashed edges correspond to paired-test studies. Black circles represent tests studied in single-test studies, whereas white circles represent tests studied in comparative studies.
We used the cervical cancer data to assess the identified DTA-NMA models, and presented the sensitivity and specificity results using forest plots. We ranked the tests based on the diagnostic odds ratio (DOR) measure that accounts for both sensitivity and specificity, and the relative sensitivity and specificity24.
Results
The database search yielded 7,190 potentially relevant citations and 41 records were located through other sources. In total, 10 articles (7 published papers and 3 dissertations) were included in this review (Figure 2), which are listed in Appendix 3. A summary of the study characteristics included in this review is available in Appendix 4.
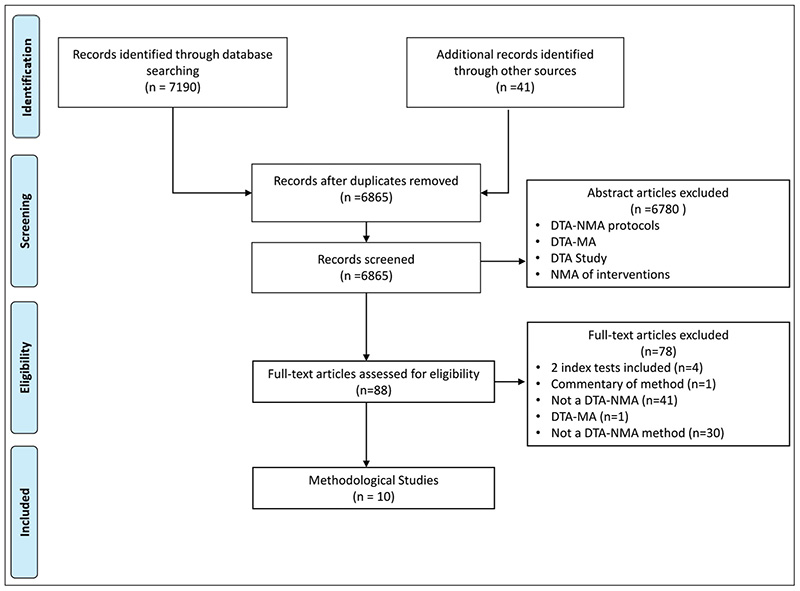
Figure 2. Study flow diagram.
We identified 4 methods to conduct a DTA-NMA of at least three tests using the 2×2 table for each index test. All models are Bayesian hierarchical DTA-NMA approaches. Below we present the identified approaches and in a separate section we present the comparative results using the illustrative example. In Table 1 we summarize the four methods, their key properties and the software they were initially developed.
Modelling multiple diagnostic tests
Hierarchical Latent Class Model (Model 1)
Accounting for the use of imperfect reference standards, where the estimated accuracy of a test may be biased, Menten and Lesaffre have introduced a contrast-based DTA-NMA model in a Bayesian framework10. Different reference standards, both perfect and imperfect, can be used within the same model. In a latent class model, the true status of the patient is an unobserved variable (diseased or non-diseased) and this unobserved variable determines the probability to test positive or negative. Prior knowledge on the accuracy of the reference test(s) can be employed to estimate these probabilities. The model uses the number of participants showing the pattern of outcomes across the tests assessed in a study instead of the 2×2 table, and considers one pair of sensitivity and specificity per test and study. The observed data are assumed to come from a multinomial distribution, and all study-specific sensitivities and specificities across tests are modeled using separate bivariate normal distributions. Using the logit transformation, the differences (contrasts) between the different tests in the network are estimated. The model estimates the within-contrast heterogeneity across studies. A limitation of the method is that correlations between tests from the same study are ignored.
Normal-binomial Model (Model 2)
Considering that each participant is being measured across multiple tests within each study, Nyaga et al. developed an arm-based two-stage hierarchical model using a two-way ANOVA model8. The model is based on the single factor design with repeated measures, and allows borrowing strength across studies to estimate sensitivity and specificity of the tests included in the network. Given the study-specific sensitivity and specificity, at the first stage the model uses two independent binomial distributions for the true positives among the diseased, and the true negatives among the non-diseased participants. Using (logit) transformations of sensitivity and specificity, a shared random-effects parameter (the within-study variance) is considered at the second stage, to allow for the intra-study correlation of sensitivity or specificity. Two sources of variation are considered: a) the within-study heterogeneity, due to variation in repeated sampling of study results, and b) the between-study heterogeneity, due to variation in the true study-specific effects. For a zero within-study variance across tests, the model reduces to separate bivariate random-effects meta-analysis models.
The model is based on the assumption that all tests could have been used in each study, but they are missing for reasons not related to their outcome (missing at random). Hence, under the intention-to-treat principle, the sensitivities and specificities of the unobserved tests are parameters that are estimated along with the other parameters in the model based on the exchangeability assumption, i.e., sensitivity and specificity are similar across studies yet not identical. While this assumption may be reasonable when a common ‘threshold effect’ exists in all cases, assuming common correlation between sensitivity and specificity across tests in a NMA of different tests at different thresholds may not be valid.
Beta-binomial model (Model 3)
Nyaga et al. suggested an arm-based NMA model based on the bivariate beta distribution7. The use of beta distribution allows for a) probabilities to be modelled on their natural scale (in contrast with Model 2), b) asymmetry in the distribution of probabilities, which is often the case for sparse data, and c) direct interpretation of probabilities, since they are modelled on their natural scale and no back-transformations are required. As in Model 2, Model 3 can incorporate studies irrespective of the studied number of arms, and is based on the assumption that tests missing from a study are missing at random.
Model 3 is a two-stage model. First, the marginal beta distributions for sensitivity and specificity are used separately. At a second stage, these distributions are linked by the Frank copula function25, which describes the correlation between sensitivity/specificity and the overdispersion due to repeated measures. Hence, the bivariate beta density describes the joint distribution of sensitivity and specificity. Different copula densities can be used, which can lead to a different bivariate beta density. However, the choice of the copula function should be based on the relationship between sensitivity and specificity. While sensitivity and specificity are usually negatively correlated, there may be cases in which they are positively correlated. In these cases, copula functions that model both negative and positive correlations are needed. Similar to Model 2, both the within-study and between-study variance are considered.
Variance component model (Model 4)
Owen et al.26 proposed an arm-based variance component model for synthesizing data on different tests at multiple thresholds, to account for the inherent correlations between multiple pairs of sensitivity and specificity data within a study. The model is an extension to the normal-binomial model by Nyaga et al.7 and can incorporate constraints on threshold effects. For example, assigning constraints on increasing test thresholds, higher test thresholds are expected to have greater sensitivity but lower specificity. The use of threshold constraints can better account for the variability due to threshold effects and better explain between-study heterogeneity.
Model 4 is a two-stage approach. At the first stage, logistic models are used to specify the arm-specific (i.e., at the specific test and threshold) sensitivity and specificity. At the second stage, each pair of logit sensitivity and logit specificity are drawn from a bivariate normal distribution with mean equal to the pooled estimates of sensitivity and specificity and variance the between-arm covariance matrix including the between-arm standard deviation in logit transformed sensitivity and specificity, and the between-arm correlation. Interactions between study and diagnostic test, due to multiple thresholds, are included in the model. Constraints on increasing test thresholds can also be applied. A limitation of the method is that sometimes the covariance matrix is unidentifiable and the model does not produce results.
Evaluation of the methods in a case-study
We analyzed the NMA of the tests for the diagnosis of CIN2+ presented in section 2.2 using the four models. For completeness, we also applied the popular meta-regression approach with the test-type as a covariate27. We fitted the model using this covariate term separately for sensitivity and specificity assuming different variances for the logit transformed sensitivities/specificities. However, this method does not account for the within-study correlation between tests, and does not properly model multi-test studies assuming that each 2×2 table belongs to a separate study.
We implemented Models 1, 2, and 3 using Stan28 and the rstan package29 within R version 3.6.3 using the Hamilton Monte Carlo (MHC) simulations. We fitted Model 4 in WinBUGS 1.4 software using the Markov Chain Monte Carlo (MCMC) simulations. We ran four chains with 100,000 draws and removed the first 1,000 draws (burn-in). To reduce autocorrelation, we applied a thinning by keeping every 10th draw. Convergence was explored through visual inspection of trace plots and when R^was lower than 1.1. Meta-regression was performed in STATA/MP 14.0 using the meqrlogit command30.
Figure 3 shows the sensitivity and specificity for the cytology, HPV DNA, and mRNA tests for CIN2+ using the NMA models. Overall, mRNA has higher sensitivity and specificity compared to cytology and HPV DNA, but these estimates are associated with higher uncertainty possibly due to the small number of studies assessing the test. The popular bivariate meta-regression model indicated the highest estimated sensitivity and specificity across tests. The beta-binomial NMA model is associated with high uncertainty in the underlying estimates, accounting probably for the variance in sensitivity and specificity that may be underestimated with the normal-binomial models. The variance component model by Owen et al, allows the estimation of sensitivity and specificity for the two thresholds LSIL+ and ASCUS+ of the cytology test. The model suggests that ASCUS+ has higher sensitivity but lower specificity compared to LSIL+. Differences in the test results across models may be due to varying estimation of heterogeneity (Tables 2 and 3).

Figure 3. Forest plot of sensitivity (a) and specificity (b) for the cytology, HPV DNA, and mRNA tests for CIN2+ using different network meta-analysis models.
According to the DOR all models suggest that mRNA has the largest likelihood of being the most accurate test followed by HPV DNA. The indirect comparison results derived from the bivariate meta-regression and Models 1, 2 and 3 suggest that mRNA and HPV-DNA tests performed better compared to the cytology test with a range in relative sensitivity 1.36-1.39 and 1.33-1.35, respectively (Table 2). However, both tests performed had similar or worse specificity than cytology (relative specificity range in mRNA 0.96-0.98 and in HPV-DNA 0.94-0.95). Model 4 suggested similar conclusions, as well as that cytology ASCUS+ had higher sensitivity than cytology LSIL+, but lower specificity. Cytology ASCUS+ had similar specificity with mRNA (relative specificity: 0.99 95% CI [0.95, 1.01]), but lower specificity than HPV-DNA test (relative specificity: 0.95 95% CI [0.94, 0.96]).
Discussion
In this review we found 10 methodological papers presenting or discussing a DTA-NMA method. Only four of the methods use the commonly available information from DTA studies, that is the true positive, false positive, true negative and false negative values per test and study. The four methods have been developed in a Bayesian hierarchical framework and relevant coding in Stan28,29 and WinBUGS31 is available in each publication.
The four approaches are associated with different key properties. First, all but the hierarachical latent class10 method are arm-based approaches. It has been suggested that arm-based methods outperform contrast-based methods, since the latter assume all tests are compared to a common reference test across studies, and requires at least two diagnostic tests to be compared within a study. Second, the arm-based approaches (i.e. normal-binomial model, beta-binomial model, and variance component model) assume that the missing tests (i.e., arms) are missing at random7,8,26. Third, the present contrast-based approach (i.e. the hierarchical latent class model) is the only method that allows for the inclusion of imperfect reference standards10. Fourth, the model presented by Owen et al.26 (i.e. the variance component model) can synthesize data for different tests at multiple thresholds, allowing for the inclusion of constraints on increasing test thresholds. Although the variance component model is the only approach to account for different thresholds across studies, it treats different test-threshold combinations as separate tests, and hence full SROC plots cannot be drawn. Fifth, all apart form the hierarchical latent class10 model account for the inherent correlations between multiple pairs of sensitivity and specificity data across tests within a study. Sixth, three8,10,26 of the four approaches, i.e. the hierarchical latent class, normal-binomial, and variance component methods, model the logit sensitivities and specificities across tests, assuming that the transformed quantities have approximately a normal distribution with a constant variance. However, when proportions are modelled, such as sensitivity and specificity, the constant variance condition is not always satisfied and variance depends on the underlying proportion. Proportions close to 0 or 1 have a variance close to zero, whereas proportions close to 0.5 have the highest variance value. This also shows that the parameter space for proportions and variances is constrained, which contradicts the unbounded and independent normally distributed parameters. Hence, a natural way to model sensitivity and specificity is to use a bivariate beta distribution, as shown by Nyaga et al.7 in the beta-binomian model, which allows for symmetry and accounts properly for overdispersion.
Additional DTA-NMA methods have been suggested using the full cross-tabulations across studies. These include multivariate approaches that can adequately model the within-study correlations across tests, and can be performed both in Bayesian and frequentist frameworks11,14,32. Although the DTA-NMA methods are an important contribution to the field of diagnostic tests, there are several limitations associated with these models. A key barrier of the methods is that as the number of diagnostic tests increases, the number of additional parameters to estimate also increases, and in these cases, complexity and convergence issues with multivariate approaches can be raised. Also, when a small number of studies is available, it might be challenging to estimate all the parameters of the model. The main limitation across all models is the lack of their availability in popular statistical software, which increases complexity of their implementation. However, the choice of the most appropriate model rests on the availability of complete data, use of similar thresholds and reference standards, number of comparator tests, and number of studies across test comparisons.
For the diagnosis of CIN2+ we found that the mRNA test was the most accurate test followed by HPV-DNA. However, both sensitivity and specificity of the mRNA test were associated with the highest uncertainty across all models. Overall, precision and estimation of between-study and within-study variability varied across models due to the differences in their key properties. Evaluation of the comparative effectiveness and safety that use primary HPV screening in comparison to cytology-based screening in asymptomatic women is another key question in cervical cancer33.
This is the first study summarizing the available DTA-NMA methods. We describe the key methodological characteristics of the DTA-NMA methods through a case example for CIN2+. To date, there are no other reviews in the literature comparing DTA-NMA methods, and hopefully our findings will facilitate investigators in forming their own judgements about the most appropriate method for their needs. We also expect that this review will help increase application of the methods in empirical DTA networks.
A limitation of our review is that we may have not retrieved all DTA-NMA methods, as some studies may have not been indexed using the search terms we selected. In order to capture the majority (if not all) of the DTA-NMA methods we developed a very sensitive literature search. Another limitation is that although we identified 10 eligible studies, we were able to assess only four DTA-NMA methods using the 2×2 table of the results of each index test against the reference standard. Methods requiring the complete cross-tables can rarely be applied in empirical examples, since this information is usually missing from the DTA publications. Finally, we explored the performance of the methods using a single case study. A comprehensive empirical comparison of all the DTA-NMA models to evaluate key properties of the methods would be a valuable addition to the literature. Simulation studies are also required to assess the performance of the methods and indicate which methods perform best in real-life meta-analytical scenarios.
Conclusions
To date, four different DTA-NMA methods have been suggested to model at least three tests using the 2×2 table for each index test. All models were developed in a Bayesian framework, but they are associated with different properties and may lead to different results, especially for sparse data. The choice of a DTA-NMA method for the comparison of multiple diagnostic tests may depend on the available data, e.g., threshold data, as well as on clinically-related factors that need to be considered in decision-making. Our empirical example on the diagnosis of CIN2+ showed that estimation and precision in sensitivity and specificity may vary depending on the choice of the method. Overall, we found that both mRNA and HPV-DNA tests outperformed cytology, and that the cytology ASCUS+ was associated with higher sensitivity but lower specificity when compared with cytology LSIL+.
Acknowledgements
We thank Dr. Antonis Athanasiou for his help with re-coding the data to construct a network of diagnostic test accuracy studies. We thank Dr. Yemisi Takwoingi and Dr. Gerta Rücker for ealier discussions at the protocol stage of this work. Finally, we would like to thank Dr. Stella Zevgiti and Ms. Eirini Pagkalidou for helping screen studies for inclusion.
This research is co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Programme «Human Resources Development, Education and Lifelong Learning 2014-2020» in the context of the project “EXTENSION OF NETWORK META-ANALYSIS FOR THE COMPARISON OF DIAGNOSTIC TESTS” (MIS 5047640).
Contributors
AAV and DM conceived and designed the study. AAV coordinated the review, screened citations, provided input in the analysis, interpreted results, and wrote a draft manuscript. ST screened citations, abstracted data, conducted analysis, interpreted results, and edited the manuscript. DM interpreted results and edited the manuscript. EvP provided input into the design, interpreted results, and edited the manuscript. All authors read and approved the final manuscript.
Declaration of Interests
The authors declare that they have no competing interests.
References
1. Irwig L, et al, Guidelines for meta-analyses evaluating diagnostic tests. Ann Intern Med, 1994. 120(8): p. 667-76.
2. Lau J, Ioannidis JP and Schmid CH, Summing up evidence: one answer is not always enough. Lancet, 1998. 351(9096): p. 123-7.
3. Lijmer JG, Leeflang M and Bossuyt PM, Proposals for a phased evaluation of medical tests. Med Decis Making, 2009. 29(5): p. E13-21.
4. Mavridis D, et al. A primer on network meta-analysis with emphasis on mental health. Evid Based Ment Health, 2015. 18(2): p. 40-6.
5. Salanti G, Indirect and mixed-treatment comparison, network, or multiple-treatments meta-analysis: many names, many benefits, many concerns for the next generation evidence synthesis tool. Res Synth Methods, 2012. 3(2): p. 80-97.
6. Lu G and Ades AE, Combination of direct and indirect evidence in mixed treatment comparisons. Stat Med, 2004. 23(20): p. 3105-24.
7. Nyaga VN, Arbyn M and Aerts M, Beta-binomial analysis of variance model for network meta-analysis of diagnostic test accuracy data. Stat Methods Med Res, 2018. 27(8): p. 2554-66.
8. Nyaga VN, Aerts M and Arbyn M, ANOVA model for network meta-analysis of diagnostic test accuracy data. Stat Methods Med Res, 2018. 27(6): p. 1766-1784.
9. Dimou NL, Adam M and Bagos PG, A multivariate method for meta-analysis and comparison of diagnostic tests. 2016. 35(20): p. 3509-23.
10. Menten J and Lesaffre E, A general framework for comparative Bayesian meta-analysis of diagnostic studies. BMC Med Res Methodol, 2015. 15: p. 70.
11. Trikalinos TA, et al, Methods for the joint meta-analysis of multiple tests. Res Synth Methods, 2014. 5(4): p. 294-312.
12. Hoyer A and Kuss O, Meta-analysis for the comparison of two diagnostic tests to a common gold standard: A generalized linear mixed model approach. Stat Methods Med Res, 2018. 27(5): p. 1410-21.
13. Hoyer A and Kuss O, Meta-analysis for the comparison of two diagnostic tests-A new approach based on copulas. Stat Med, 2018. 37(5): p. 739-748.
14. Cheng W SC, Trikalinos TA, Gatsonis CA, Network meta-analysis of diagnostic accuracy studies. Ph.D. Dissertation, Brown University, DOI: 10.7301/Z0HX1B3W. 2016.
15. Ma X et al, A Bayesian hierarchical model for network meta-analysis of multiple diagnostic tests. Biostatistics, 2018. 19(1): p. 87-102.
16. Veroniki AA, et al, Chapter 19 “Challenges in comparative meta-analysis of the accuracy of multiple diagnostic tests.”, in Meta-Research, EE and VAA, Editors. 2021, Springer.
17. Veroniki AA, et al., Protocol for a scoping review to identify all available NMA-DTA models. https://esm.uoi.gr/wp-content/uploads/2020/05/DiagnosNMA_protocol.pdf, 2019.
18. Rücker G, Network Meta-Analysis of Diagnostic Test Accuracy Studies, in Diagnostic Meta-Analysis, G. Biondi-Zoccai, Editor. 2018, Springer: Cham.
19. World Health Organization WHO. Human papillomavirus (HPV) and cervical cancer. 2019.
20. Bowden SJ, et al, The use of human papillomavirus DNA methylation in cervical intraepithelial neoplasia: A systematic review and meta-analysis. EBioMedicine, 2019. 50: p. 246-59.
21. Kyrgiou M, et al, Fertility and early pregnancy outcomes after conservative treatment for cervical intraepithelial neoplasia. Cochrane Database Syst Rev, 2015(9): p. CD008478.
22. Kyrgiou M, et al, Adverse obstetric outcomes after local treatment for cervical preinvasive and early invasive disease according to cone depth: systematic review and meta-analysis. BMJ, 2016. 354: p. i3633.
23. Koliopoulos G, et al, Cytology versus HPV testing for cervical cancer screening in the general population. Cochrane Database of Systematic Reviews, 2017(8).
24. Glas AS, et al., The diagnostic odds ratio: a single indicator of test performance. J Clin Epidemiol, 2003. 56(11): p. 1129-35.
25. Frank MJ, “On the simultaneous associativity of F(x, y) and x + y – F(x, y)..” Aequationes mathematicae 19 (1979): 194-226. <http://eudml.org/doc/136825>.
26. Owen RK, et al., Network meta-analysis of diagnostic test accuracy studies identifies and ranks the optimal diagnostic tests and thresholds for health care policy and decision-making. Journal of Clinical Epidemiology, 2018. 99: p. 64-74.
27. Reitsma JB, et al, Bivariate analysis of sensitivity and specificity produces informative summary measures in diagnostic reviews. J Clin Epidemiol, 2005. 58(10): p. 982-90.
28. Carpenter B, et al, Stan: A Probabilistic Programming Language. Journal of Statistical Software; Vol 1, Issue 1 (2017), 2017.
29. Stan Development Team, “RStan: the R interface to Stan.” R package version 2.21.2, http://mc-stan.org/. 2020.
30. Rabe-Hesketh S SA, Multilevel and longitudinal modeling using Stata. Stata Press, College Station, TX, 2008.
31. Lunn DJ, et al, WinBUGS – A Bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing, 2000. 10(4): p. 325-37.
32. Dimou NL, Adam M, and Bagos PG, A multivariate method for meta-analysis and comparison of diagnostic tests. Stat Med, 2016. 35(20): p. 3509-23.
33. Schmucker C, et al, Cervical Cancer Screening with Human Papillomavirus Testing. PROSPERO: International prospective register of systematic reviews, 2020.